Kramers' opacity law

Kramers' opacity law describes the behavior of the opacity in terms of the ambient density and temperature when the opacity is dominated by bound-free absorption (the ionization of a bound electron) or free-free absorption (also called bremsstrahlung).^[1] It is named after the Dutch physicist Hendrik Kramers, who first derived the form in 1923.^[2]

The general functional form of the opacity law is

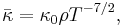
$\bar{\kappa} = \kappa_0 \rho T^{-7/2},$

where 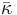$\bar{\kappa}$ is the average opacity, 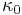$\kappa_0$ is a parameter that encapsulates fractional abundances and quantum mechanical corrections, $\rho$ is the density, and $T$ is the temperature. This form alone is useful for understanding how changes in either the density or temperature will affect the opacity, which in turn is important in understanding radiative transfer, particularly in stellar atmospheres.^[3]

The specific forms for bound-free and free-free are

Bound-free: 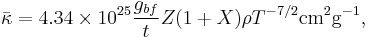$\bar{\kappa} = 4.34 \times 10^{25} \frac{g_{bf}}{t}Z(1%2BX) \rho T^{-7/2} {\rm cm^2 g^{-1}},$

Free-free: 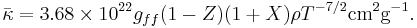$\bar{\kappa} = 3.68 \times 10^{22} g_{ff}(1 - Z)(1 %2B X) \rho T^{-7/2} {\rm cm^2 g^{-1}}.$

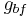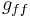Here, $g_{bf}$ and $g_{ff}$ are the Gaunt factors associated with bound-free and free-free transitions, respectively, and are quantum mechanical correction terms. The $t$ is an additional correction factor, typically having a value between 1 and 100. $Z$ is the fractional abundance by mass of elements heavier than hydrogen, and $X$ is the fractional abundance by mass of hydrogen.^[2]

References

^ Phillips (1999), p. 92.
^ ^a ^b Carroll (1996), p. 274.
^ Carroll (1996), p. 274–276.

Bibliography

Carroll, Bradley; Ostlie, Dale (1996). Modern Astrophysics. Addison-Wesley. http://books.google.com/books?id=yXR_QgAACAAJ.
Phillips, A. C. (1999). The Physics of Stars. Wiley. http://books.google.com/books?id=4CZpQgAACAAJ.